그래프와 서로소 집합



10.3 개선된 서로소 집합 알고리즘 코드
#include <bits/stdc++.h>
using namespace std;
// 노드의 개수(V)와 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
int v, e;
int parent[100001]; // 부모 테이블 초기화
// 특정 원소가 속한 집합을 찾기
int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) return x;
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
int main(void) {
cin >> v >> e;
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
// Union 연산을 각각 수행
for (int i = 0; i < e; i++) {
int a, b;
cin >> a >> b;
unionParent(a, b);
}
// 각 원소가 속한 집합 출력하기
cout << "각 원소가 속한 집합: ";
for (int i = 1; i <= v; i++) {
cout << findParent(i) << ' ';
}
cout << '\n';
// 부모 테이블 내용 출력하기
cout << "부모 테이블: ";
for (int i = 1; i <= v; i++) {
cout << parent[i] << ' ';
}
cout << '\n';
}
10.4 서로소 집합을 활용한 사이클 판별 코드
#include <bits/stdc++.h>
using namespace std;
// 노드의 개수(V)와 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
int v, e;
int parent[100001]; // 부모 테이블 초기화
// 특정 원소가 속한 집합을 찾기
int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) return x;
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
int main(void) {
cin >> v >> e;
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
bool cycle = false; // 사이클 발생 여부
for (int i = 0; i < e; i++) {
int a, b;
cin >> a >> b;
// 사이클이 발생한 경우 종료
if (findParent(a) == findParent(b)) {
cycle = true;
break;
}
// 사이클이 발생하지 않았다면 합집합(Union) 연산 수행
else {
unionParent(a, b);
}
}
if (cycle) {
cout << "사이클이 발생했습니다." << '\n';
}
else {
cout << "사이클이 발생하지 않았습니다." << '\n';
}
}
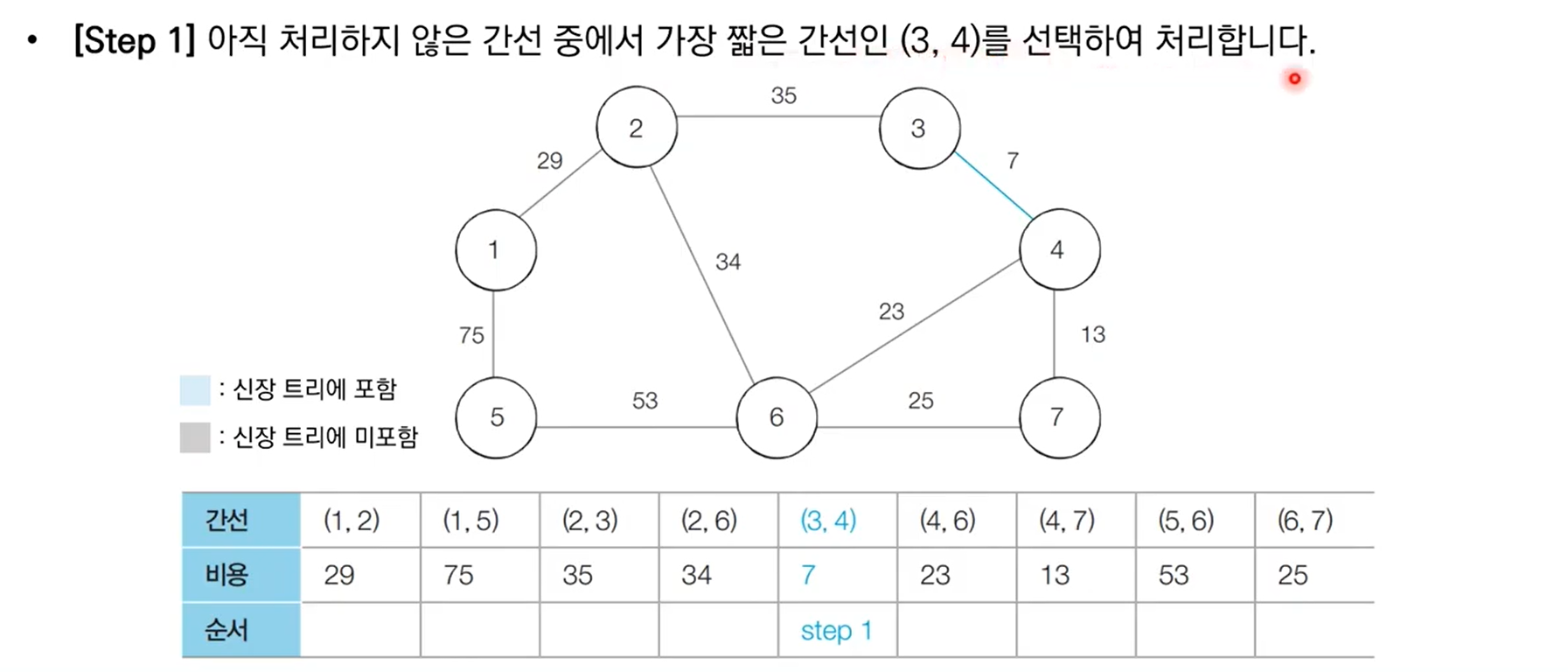
크루스칼 알고리즘

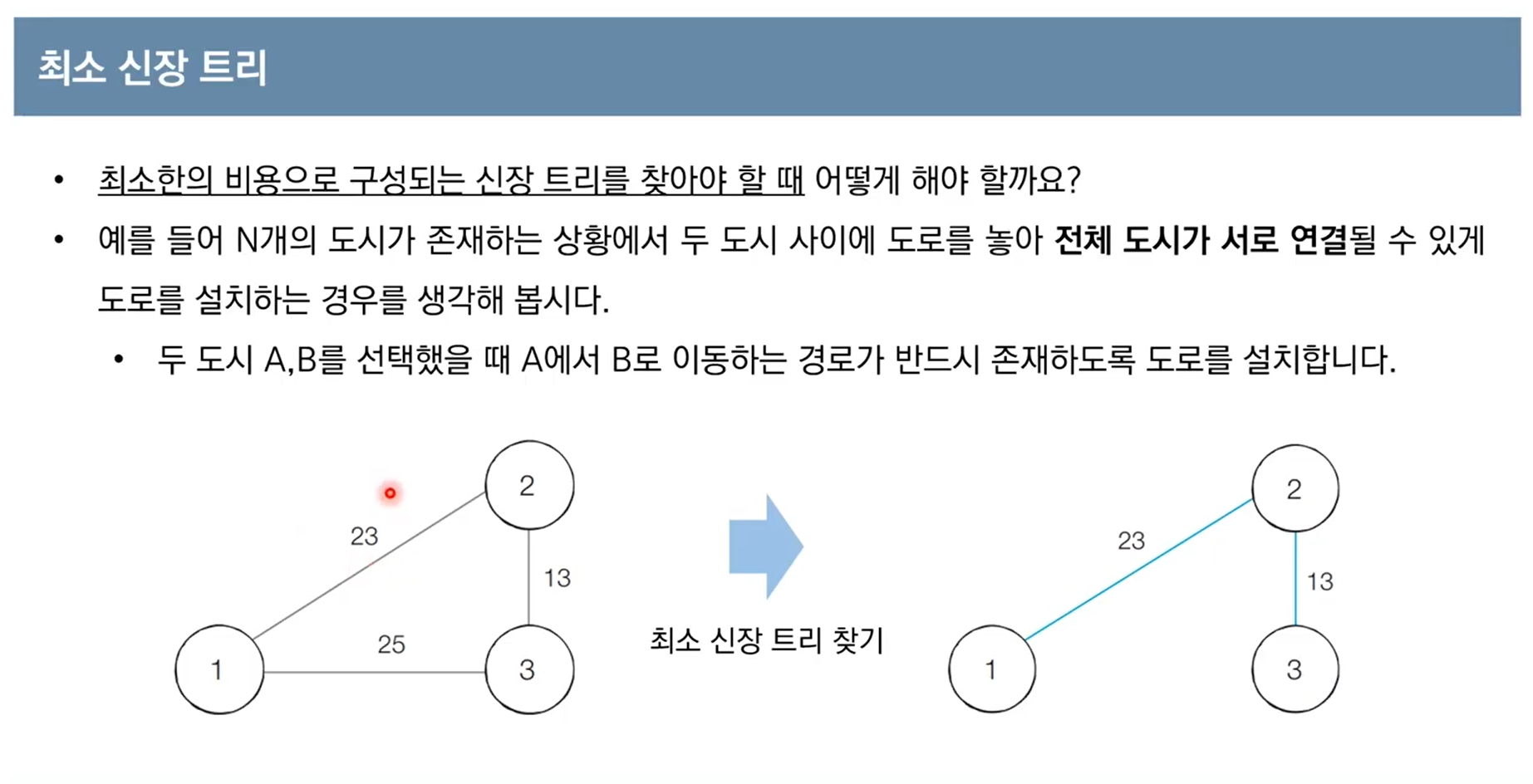
크루스칼 알고리즘 동작 방식: 간선을 하나씩 확인하면서 신장 트리에 포함을 시킬지 안 시킬지 결정










10.5 크루스칼 알고리즘 구현
#include <bits/stdc++.h>
using namespace std;
// 노드의 개수(V)와 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
int v, e;
int parent[100001]; // 부모 테이블 초기화
// 모든 간선을 담을 리스트와, 최종 비용을 담을 변수
vector<pair<int, pair<int, int> > > edges;
int result = 0;
// 특정 원소가 속한 집합을 찾기
int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) return x;
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
int main(void) {
cin >> v >> e;
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
// 모든 간선에 대한 정보를 입력 받기
for (int i = 0; i < e; i++) {
int a, b, cost;
cin >> a >> b >> cost;
// 비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
edges.push_back({cost, {a, b}});
}
// 간선을 비용순으로 정렬
sort(edges.begin(), edges.end());
// 간선을 하나씩 확인하며
for (int i = 0; i < edges.size(); i++) {
int cost = edges[i].first;
int a = edges[i].second.first;
int b = edges[i].second.second;
// 사이클이 발생하지 않는 경우에만 집합에 포함
if (findParent(a) != findParent(b)) {
unionParent(a, b);
result += cost;
}
}
cout << result << '\n';
}

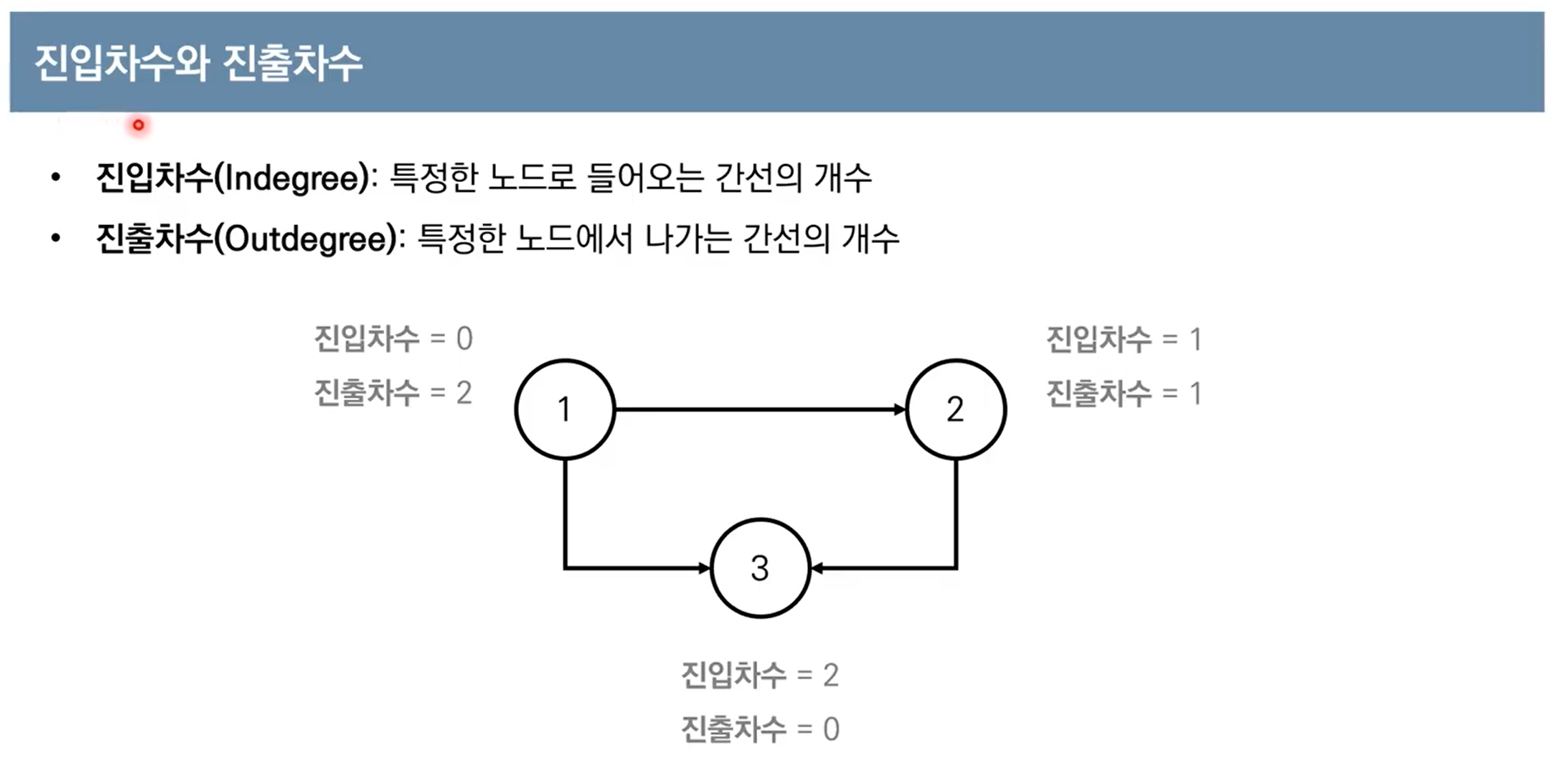
위상 정렬

위상 정렬을 다루기 전에, 그래프 관련 자료구조에 자주 나타나는 개념들을 알아보자.



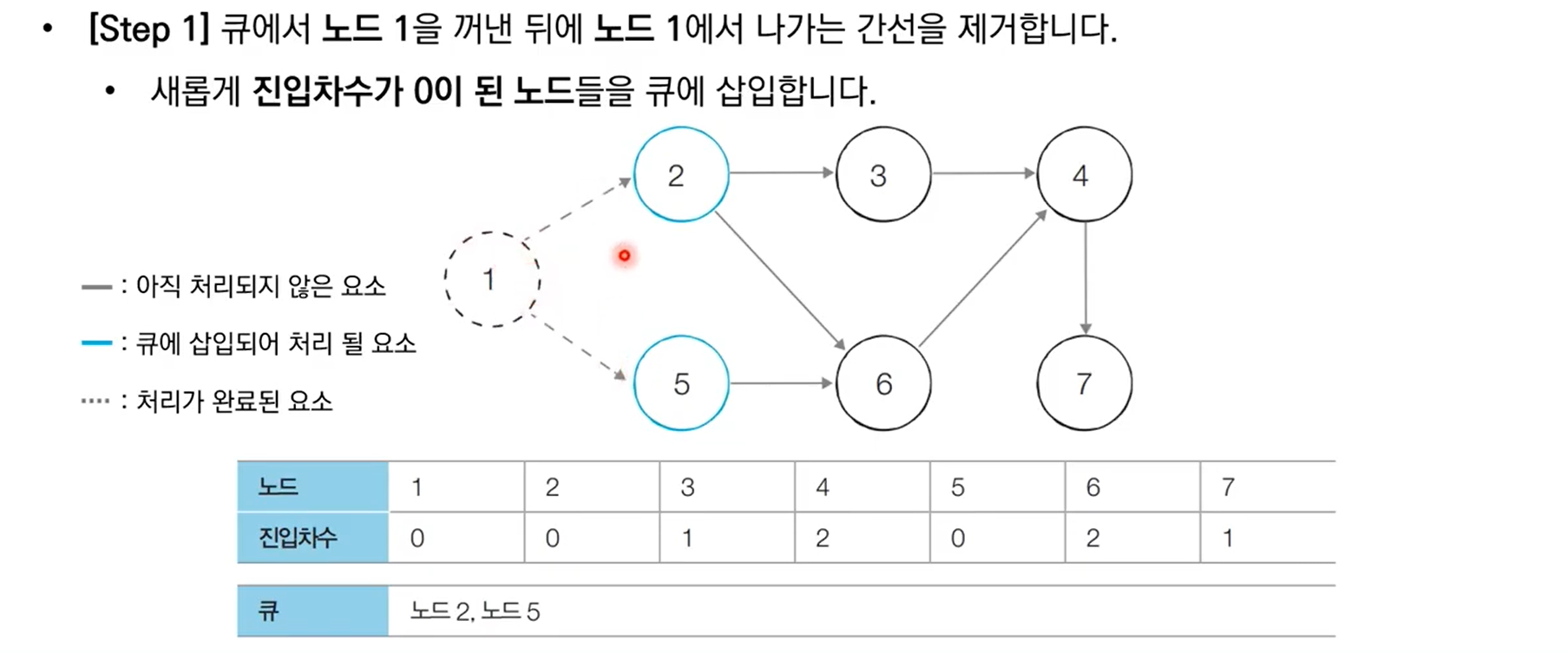




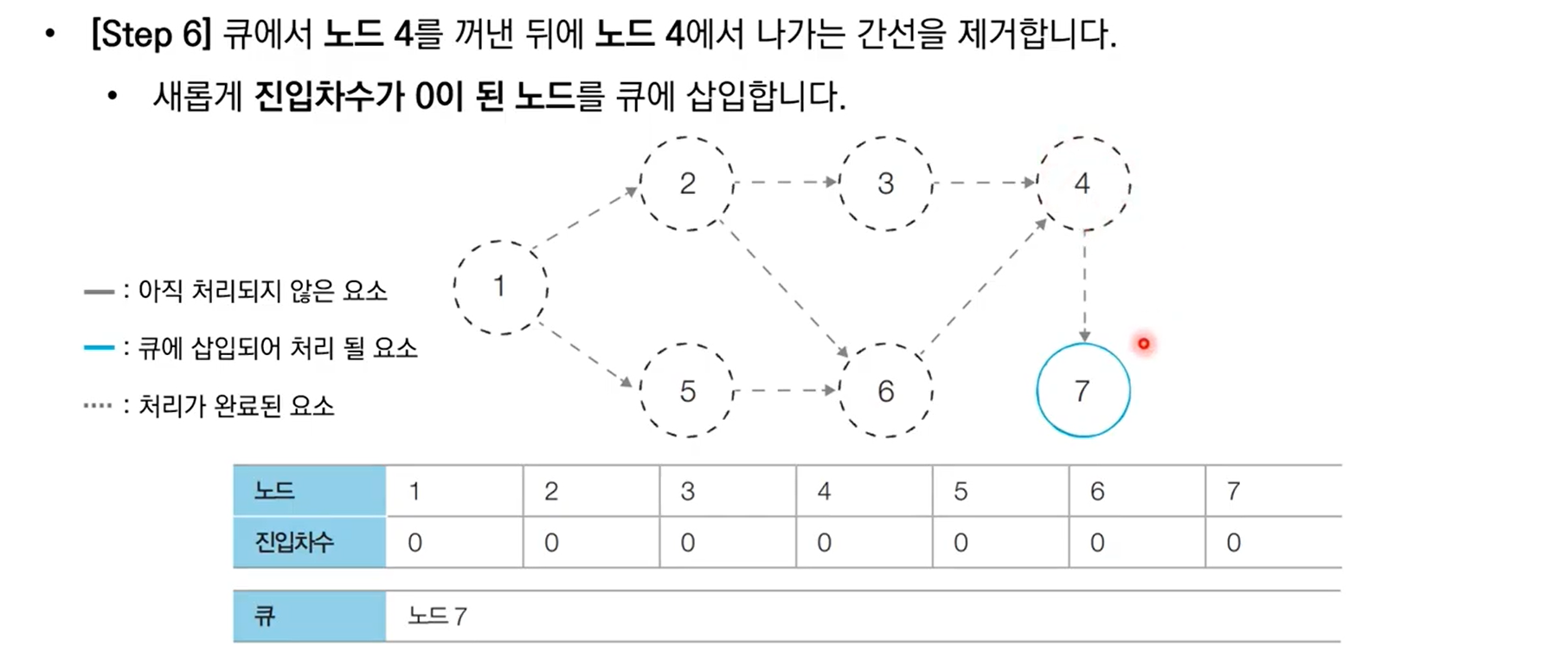

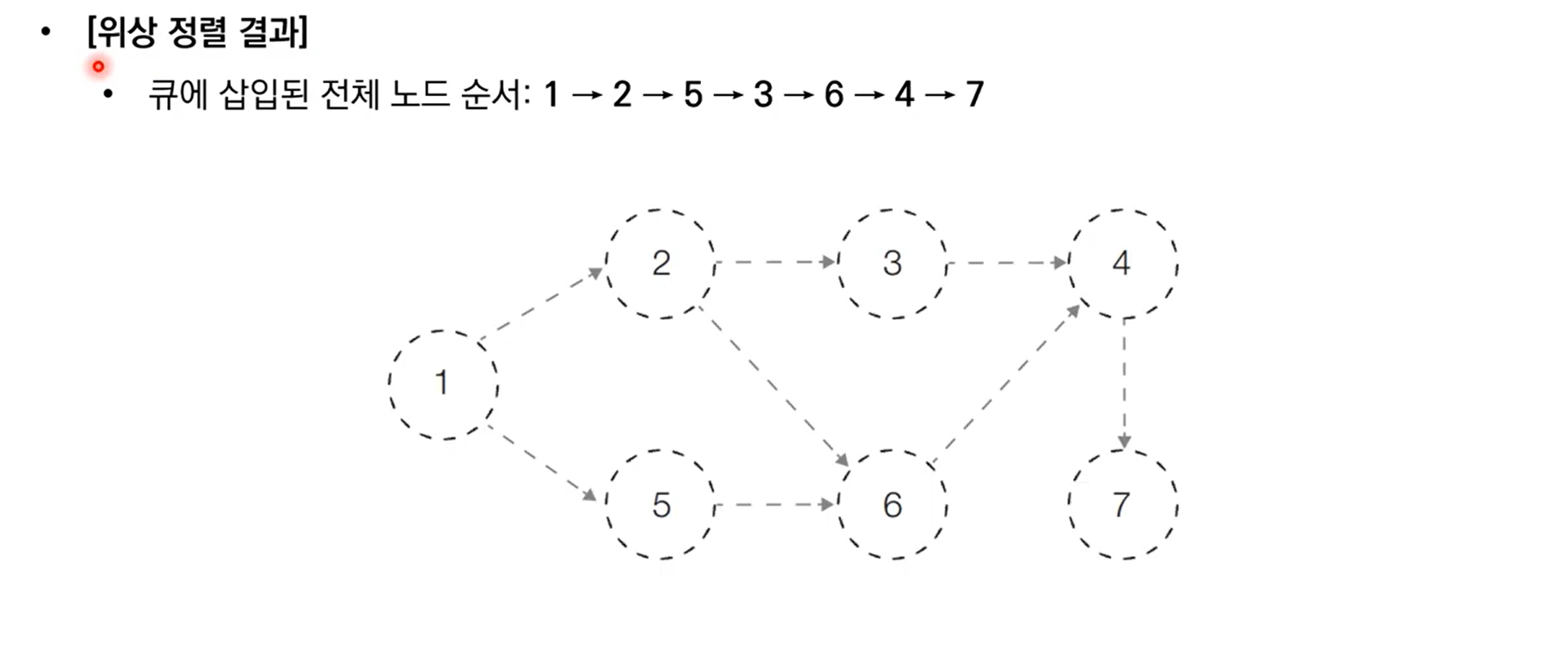

10.6 위상 정렬 알고리즘 구현
#include <bits/stdc++.h>
using namespace std;
// 노드의 개수(V)와 간선의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
int v, e;
// 모든 노드에 대한 진입차수는 0으로 초기화
int indegree[100001];
// 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
vector<int> graph[100001];
// 위상 정렬 함수
void topologySort() {
vector<int> result; // 알고리즘 수행 결과를 담을 리스트
queue<int> q; // 큐 라이브러리 사용
// 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for (int i = 1; i <= v; i++) {
if (indegree[i] == 0) {
q.push(i);
}
}
// 큐가 빌 때까지 반복
while (!q.empty()) {
// 큐에서 원소 꺼내기
int now = q.front();
q.pop();
result.push_back(now);
// 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for (int i = 0; i < graph[now].size(); i++) {
indegree[graph[now][i]] -= 1;
// 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if (indegree[graph[now][i]] == 0) {
q.push(graph[now][i]);
}
}
}
// 위상 정렬을 수행한 결과 출력
for (int i = 0; i < result.size(); i++) {
cout << result[i] << ' ';
}
}
int main(void) {
cin >> v >> e;
// 방향 그래프의 모든 간선 정보를 입력 받기
for (int i = 0; i < e; i++) {
int a, b;
cin >> a >> b;
graph[a].push_back(b); // 정점 A에서 B로 이동 가능
// 진입 차수를 1 증가
indegree[b] += 1;
}
topologySort();
}'알고리즘 > 이것이 코딩 테스트다' 카테고리의 다른 글
| [이코테/C++] 음료수 얼려 먹기 (0) | 2022.05.31 |
|---|---|
| 09. 최단 경로 (0) | 2022.05.10 |
| 08: 다이나믹 프로그래밍 (0) | 2022.03.27 |
| 07: 이진 탐색 (0) | 2022.03.25 |
| 06: 정렬 (0) | 2022.03.20 |
